Dennis is a hard-working business professional who enjoys spending time with his family and friends. He likes to stay active, and loves playing sports. Stephanie is always looking for new challenges and opportunities to grow both personally and professionally.
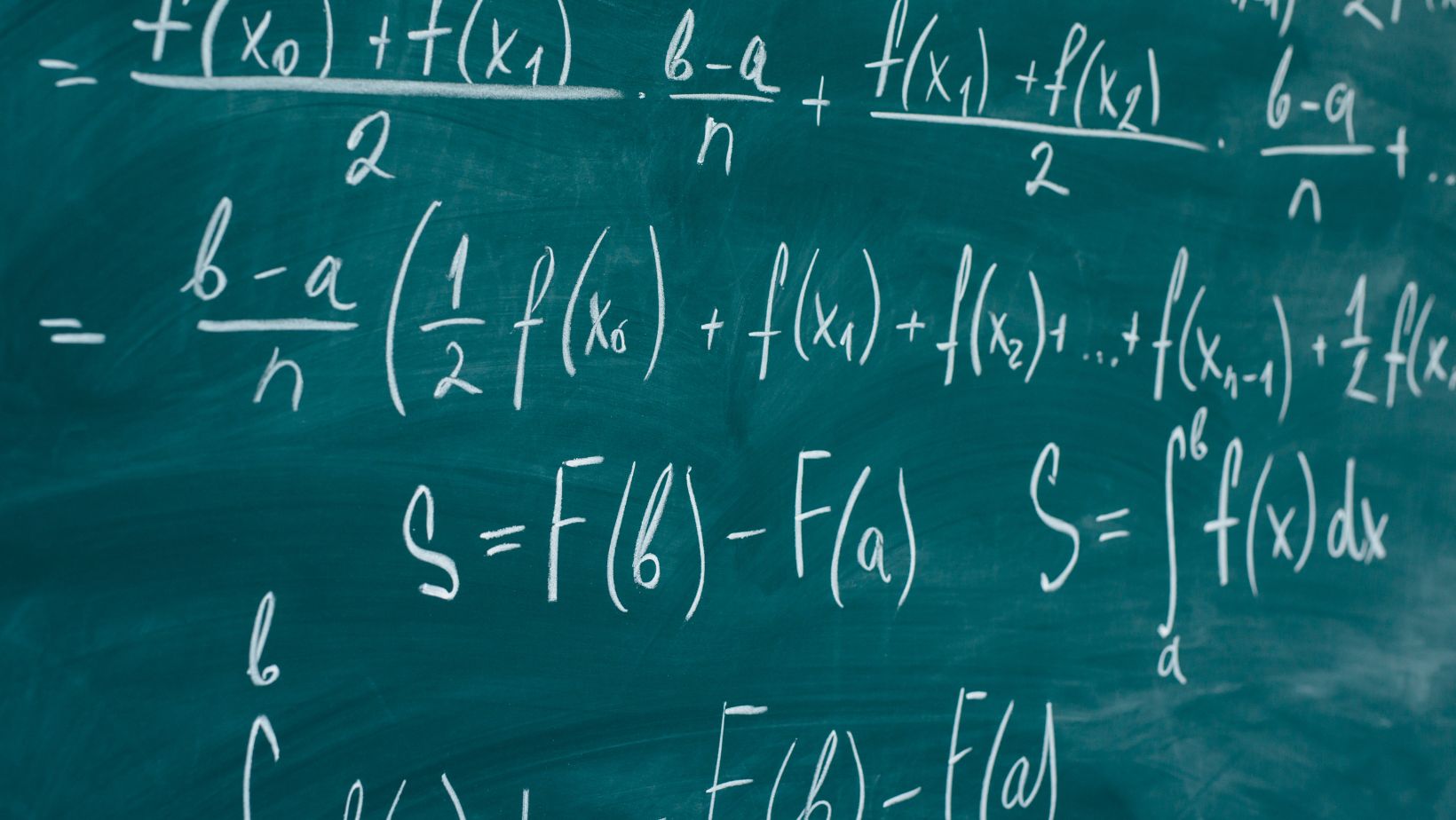
Integrals and derivatives are foundational concepts in calculus, each offering unique insights and tools for analyzing functions. In this article, we will delve into the realm of the derivative of integrals and uncover the four fundamental rules that govern this fascinating relationship. These rules not only provide a deeper understanding of function behavior but also equip us with powerful techniques for solving complex problems across a wide range of disciplines.
Whether you are a calculus enthusiast or a student navigating the intricacies of mathematical analysis, join us on this exploration of the rules for the derivative of integrals and enhance your grasp of this essential aspect of calculus. For an in-depth understanding of the derivative of integrals, visit https://solvelymath.com/articles/Integral-Derivative/.
4 Fundamental Rules Of Derivative Of Integrals
1. Fundamental Theorem of Calculus Part 1
At the heart of calculus lies the Fundamental Theorem of Calculus Part 1 (FTC Part 1), which establishes a fundamental connection between integration and differentiation.
It states that if f(x) is a continuous function on the interval [a, b] and F(x) is an antiderivative of f(x) on [a, b], then the definite integral of f(x) over [a, b] can be evaluated by simply subtracting the values of the antiderivative at the endpoints:
∫[a, b] f(x) dx = F(b) – F(a)
d/dx ∫[a, x] f(t) dt = f(x)
This theorem forms the cornerstone of calculus, providing a straightforward method for computing definite integrals.
2. Variable Upper and Lower Limits
In many cases, the limits of integration in an integral may not be constant but rather functions of another variable. In such scenarios, the Leibniz Rule, also known as Differentiation under the Integral Sign, comes into play. It allows us to differentiate an integral with respect to a parameter that appears in the limits of integration. Mathematically, it can be expressed as:
d/dx (∫[g(x), h(x)] f(t) dt) = f(h(x)) * h'(x) – f(g(x)) * g'(x)
This rule is particularly useful in problems involving changing boundaries or dynamic systems.
3. Leibniz Rule (Differentiation under the Integral Sign)
Leibniz Rule, a powerful tool in calculus, allows us to differentiate an integral with respect to a parameter that appears under the integral sign. Formally, it states:
d/dx (∫[a(x), b(x)] f(x, t) dt) = ∫[a(x), b(x)] ∂f(x, t)/∂x dt + f(x, b(x)) * b'(x) – f(x, a(x)) * a'(x)
This rule finds applications in various fields, including physics, engineering, and economics, where integrals with changing parameters are common.
4. Constant Limits of Integration
When the limits of integration are constant, and the integrand depends solely on x, the derivative of the integral equals zero:
d/dx (∫[a, b] f(x) dx) = 0
Conclusion
The derivative of integrals is governed by several fundamental rules that underpin the intricate relationship between integration and differentiation. From the Fundamental Theorem of Calculus Part 1 to the Leibniz Rule and beyond, these rules provide a framework for computing derivatives of integrals in various contexts. Mastering these rules not only enhances our understanding of calculus but also equips us with powerful tools for solving real-world problems across diverse fields.
